Concept:-
Sorting is a common activity in the programming work. Merge-Sort is one of the best implementation for sorting, since its running on O(nlogn) - which is the best run-time available for sorting.It is based on Divide-and-conquer paradigm. The algorithm divides the array in two halves in each step and recursively calls itself on the two halves. And then merges two sorted halves. The mergeArray() function is used to merge two sorted arrays.
Following is outline of Merge Sort Procedure:
MergeSort(arr[], l, r)
If r > l
1. Find the middle point to divide the array into two halves:
middle m = (l+r)/2
2. Call mergeSort for first half:
Call mergeSort(arr, l, m)
3. Call mergeSort for second half:
Call mergeSort(arr, m+1, r)
4. Merge the two halves sorted in step 2 and 3:
Call merge(arr, l, m, r)
Sorce Example
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace ConsoleDemoApp
{
class MergeSort
{
/* Procedure for merging two sorted array. */
static void Main(string[] args)
{
Console.Write("\nA Merg Sort Algorithm program in c#");
Console.Write("\n\nEnter the total number of elements of Array: ");
int max = Convert.ToInt32(Console.ReadLine());
int[] IntArray = new int[max];
for (int i = 0; i < max; i++)
{
Console.Write("\nEnter {" + (i + 1).ToString() + "} element: ");
IntArray[i] = Convert.ToInt32(Console.ReadLine());
}
Console.Write("\nArray Elements Before Sorting \n");
Console.Write("\n");
for (int k = 0; k < max; k++)
Console.Write(IntArray[k] + " ");
Console.Write("\n");
// Calling Merge Procedure
mergesort(IntArray, 0, IntArray.Length - 1);
// Printing Sorted array. after merge sort
Console.Write("\nArray Elements After Sorting \n");
Console.Write("\n");
foreach (int a in IntArray)
{
Console.Write(a + " ");
}
Console.ReadKey();
}
static void mergeArray(int[] arr, int start, int mid, int end)
{
/* Create a temporary array for stroing merged array (Length of temp array will be
* sum of size of both array to be merged)*/
int[] temp = new int[end - start + 1];
int i = start, j = mid + 1, k = 0;
// Now traverse both array simultaniously and store the smallest element of both to temp array
while (i <= mid && j <= end)
{
if (arr[i] < arr[j])
{
temp[k] = arr[i];
k++;
i++;
}
else
{
temp[k] = arr[j];
k++;
j++;
}
}
// If there is any element remain in first array then add it to temp array
while (i <= mid)
{
temp[k] = arr[i];
k++;
i++;
}
// If any element remain in second array then add it to temp array
while (j <= end)
{
temp[k] = arr[j];
k++;
j++;
}
// Now temp has merged sorted element of both array
// Traverse temp array and store element of temp array to original array
k = 0;
i = start;
while (k < temp.Length && i <= end)
{
arr[i] = temp[k];
i++;
k++;
}
}
// Recursive Merge Procedure
static void mergesort(int[] arr, int start, int end)
{
if (start < end)
{
int mid = (end + start) / 2;
mergesort(arr, start, mid);
mergesort(arr, mid + 1, end);
mergeArray(arr, start, mid, end);
}
}
}
}
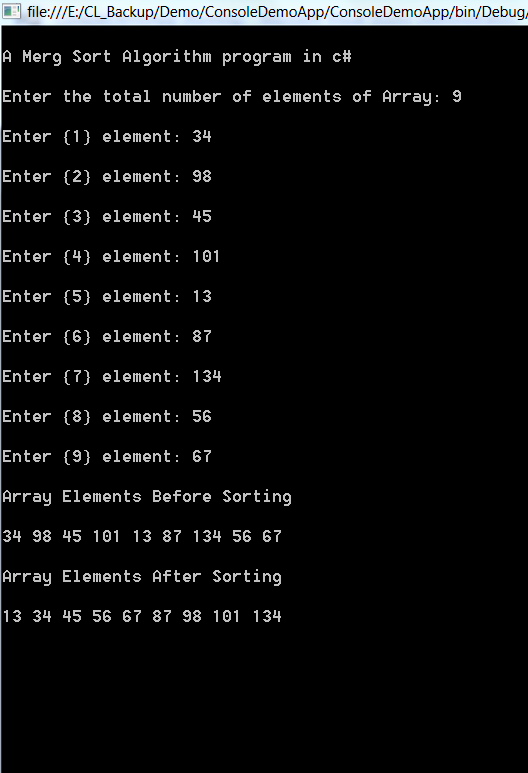
Output